Constantemente escuchamos el término crecimiento. En la actual coyuntura política y económica es empleado como sinónimo de progreso y desarrollo, produciéndonos una sensación positivista tal, que nos equivale a la solución de todos los problemas. Se crea la idea común de que no hay un límite, de que se puede seguir creciendo.
Si existiese la posibilidad de un crecimiento continuo podría ser beneficioso, pero ¿ durante cuánto tiempo se puede continuar creciendo?.
En un mundo físico existen límites, y éstos se demuestran con las matemáticas del crecimiento constante, la función exponencial. El cálculo exponencial, o es poco comprendido o simplemente es desatendido por la gente que conforman la política y el sistema financiero, ya que su conocimiento te permite entender y poder anticiparte a las consecuencias del crecimiento. En palabras del escritor Aldous Huxley, "Ciertos acontecimientos no dejan de repetirse porque son ignorados".
La función exponencial describe el crecimiento constante cuando su ritmo porcentual es fijo por unidad de tiempo. Se expresa con la siguiente ecuación;
N = N0 * e^kt
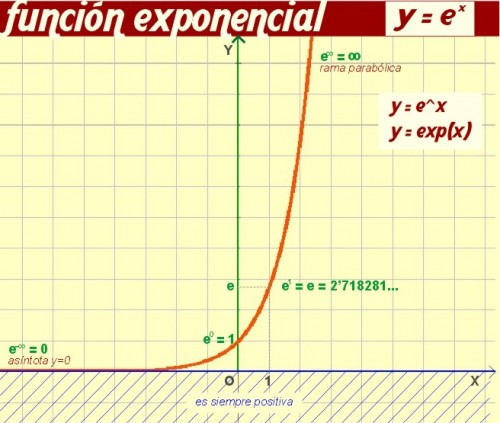 |
| Función exponencial. Fuente:yair.es |
Para ilustrar de una manera muy sencilla algunas propiedades importantes del crecimiento exponencial, lo haré con dos ejemplos;
La leyenda del ajedrez
Cuenta una leyenda que el ajedrez fue inventado por un matemático para diversión del rey al que prestaba sus servicios. El soberano, en agradecimiento, le ofreció la recompensa que quisiera. El matemático solicitó un "insignificante" premio.
La retribución solicitada por el inventor fue que le entregase la cantidad de granos de trigo que se obtienen al colocar 1 grano en el primer casillero del tablero de ajedrez, 2 en el segundo, 4 por el tercero, 8 en el cuarto y así, duplicando en cada casilla la cantidad de granos del anterior, hasta llegar al final del tablero, el casillero número 64.
El inmensamente rico rey se sorprendió ante la solicitud de tan modesto premio, y accedió gratamente a recompensarle. La sorpresa vino cuando los matemáticos reales hicieron las cuentas para saldar el pedido. La suma total en la última casilla ascendía a 18.446.744.073.709.551.615 granos de trigo. Tendiendo en cuenta un peso medio del grano a 0,03 kg el resultado era de aproximadamente 553.400 millones de toneladas de trigo. En el año 2012 la producción mundial de trigo ha sido de 672 millones de toneladas, por lo que para satisfacer el premio, se necesitaba la cosecha mundial de más de 800 años.

 |
| Crecimiento exponencial.Fuente: wikipedia |
El crecimiento bacteriano se basa en un proceso llamado fisión binaria. Es una forma de reproducción por el que, si no se produce ningún tipo de mutación, una bacteria se divide en dos células genéticamente idénticas a la célula original. De este modo se genera una duplicación de la población mediante un crecimiento exponencial.
Imaginemos un tipo de bacterias que se duplican cada minuto. A las 12:00 horas hay una bacteria dentro de una probeta. Una hora después la probeta está llena de bacterias.
Pregunta - ¿En qué momento estará ocupada en un 50% la probeta ?
Respuesta - A las 12:59 horas.
Efectivamente un minuto antes de la hora, debido a que se duplican, existen la mitad de bacterias.
Pregunta - Y dos minutos antes de la hora, ¿cuánto espacio ocuparán?
Respuesta - A las 12:58 horas, la probeta está un 25% llena y un 75% vacía.
Ahora sigamos con el experimento, colocando 3 probetas vacías a continuación. Si a las 13:00 horas estaba llena la primera probeta,
Pregunta - ¿En qué momento estarán ocupadas las 4 probetas?
Respuesta - A las 13:02 horas.
Resumen del experimento
- 12:59 h = Probeta 1 al 50%
- 13:00 h = Probeta 1 al 100%
- 13:01 h = Probetas 1 y 2 al 100%
- 13:02 h = Probetas 1,2,3 y 4 al 100%

| Probetas de laboratorio. Fuente: fullquimica.com |
Otra base útil para expresar el crecimiento exponencial es el tiempo de duplicación, que se refiere al tiempo necesario para que la cantidad que se considera duplique su valor cuando aumenta a una tasa de crecimiento constante k. A partir de la ecuación anterior, se puede demostrar una aproximación para estimar que el tiempo de duplicación sería;
T2 = 1/k * ln 2 = 0,693 / k
Si el ritmo de crecimiento k se expresa como un porcentaje, r = k / 100%, el tiempo de duplicación T2 es aproximadamente;
T2 = 70 / r
Con esta sencilla ecuación se puede estimar de manera rápida y precisa a partir de un porcentaje de crecimiento dado, el tiempo en el que se duplica el valor.
Sintetizando, los puntos más importantes de las matemáticas del crecimiento exponencial son;
- El crecimiento constante o estacionario se presenta siempre que el ritmo de crecimiento de una cantidad es proporcional a la misma.
- Se caracteriza por un tiempo de duplicación constante.
- En cada tiempo de duplicación, la cantidad de crecimiento es mayor que la totalidad de todo el crecimiento precedente.
- El crecimiento incluso durante un número no muy grande de tiempos de duplicación da unos resultados astronómicamente grandes.
- Si el consumo de un determinado recurso está creciendo constantemente, la existencia de nuevas y enormes reservas sólo permitirán un pequeño alargamiento del período de crecimiento constante con ese ritmo de consumo.
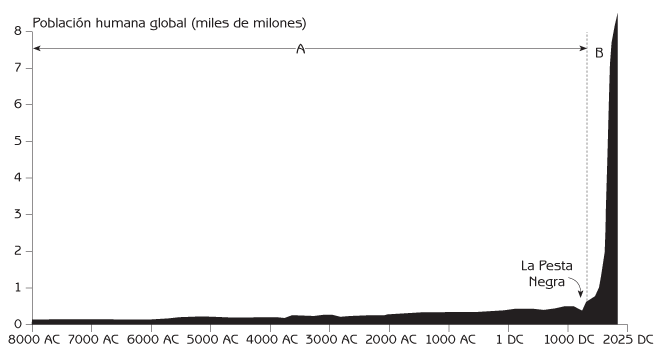 |
| Crecimiento exponencial población. Fuente: gerrymarten.com |
Para completar la exposición, os recomiendo visionar el siguiente extracto, correspondiente a las implicaciones del crecimiento exponencial en la crisis energética, del vídeo Aritmética, Población y Energía basado en la adaptación actualizada de la conferencia "Fundamentos olvidados de la crisis energética" del profesor de física Albert A.Bartlett.
El actual sistema económico, político y social está fundamentado en la expansión
económica sin fin y en mejorar los niveles de vida. Durante los últimos años, una proporción relevante del
crecimiento económico y la creación de riqueza se basó en el dinero
prestado y en la especulación, creando como principal herramienta de desarrollo el endeudamiento. La deuda permite a la sociedad comprar algo en el presente con la promesa de devolver en el futuro el préstamo más unos intereses que también necesitan del constante crecimiento.
El crecimiento también se basó en un uso insostenible de recursos naturales no renovables como el petróleo y el agua, con unas políticas perjudiciales para el medio ambiente. Es sobrecogedor evidenciar la semejanza de los problemas del sistema financiero, el daño medioambiental irreversible y la escasez de recursos tan vitales como los alimentos, el agua y el petróleo. La sociedad ha tomado prestado los bienes venideros en el presente y ha trasladado los problemas al futuro, buscando beneficios a corto plazo a expensas de riesgos que, aunque no evidentes de inmediato, surgirían más adelante. En un mundo físico, es insostenible.
El crecimiento también se basó en un uso insostenible de recursos naturales no renovables como el petróleo y el agua, con unas políticas perjudiciales para el medio ambiente. Es sobrecogedor evidenciar la semejanza de los problemas del sistema financiero, el daño medioambiental irreversible y la escasez de recursos tan vitales como los alimentos, el agua y el petróleo. La sociedad ha tomado prestado los bienes venideros en el presente y ha trasladado los problemas al futuro, buscando beneficios a corto plazo a expensas de riesgos que, aunque no evidentes de inmediato, surgirían más adelante. En un mundo físico, es insostenible.
El decrecimiento o la ausencia de crecimiento no ha de plantearse como un problema. Puede incluso ser beneficioso para el medio ambiente, los ecosistemas y la conservación de recursos naturales escasos.
Espero que todas estas explicaciones sobre la función exponencial puedan servir para que cada vez que se pronuncie el término "crecimiento", podáis valorar y pensar en las posibles consecuencias de lo que están hablando y no dejéis que manipulen la mente y el comportamiento de nadie.
Espero que todas estas explicaciones sobre la función exponencial puedan servir para que cada vez que se pronuncie el término "crecimiento", podáis valorar y pensar en las posibles consecuencias de lo que están hablando y no dejéis que manipulen la mente y el comportamiento de nadie.

No hay comentarios:
Publicar un comentario